Rahasia Angka 0
29/11/2013 12:13Ratusan tahun yang lalu, manusia hanya mengenal 9 lambang bilangan yakni 1, 2, 2, 3, 5, 6, 7, 8, dan 9. Kemudian, datang angka 0, sehingga jumlah lambang bilangan menjadi 10 buah. Tidak diketahui siapa pencipta bilangan 0, bukti sejarah hanya memperlihatkan bahwa bilangan 0 ditemukan pertama kali dalam zaman Mesir kuno. Waktu itu bilangan nol hanya sebagai lambang. Dalam zaman modern, angka nol digunakan tidak saja sebagai lambang, tetapi juga sebagai bilangan yang turut serta dalam operasi matematika. Kini, penggunaan bilangan nol telah menyusup jauh ke dalam sendi kehidupan manusia. Sistem berhitung tidak mungkin lagi mengabaikan kehadiran bilangan nol, sekalipun bilangan nol itu membuat kekacauan logika. Mari kita lihat.
Nol, penyebab komputer macet
Pelajaran tentang bilangan nol, dari sejak zaman dahulu sampai sekarang selalu menimbulkan kebingungan bagi para pelajar dan mahasiswa, bahkan masyarakat pengguna. Mengapa? Bukankah bilangan nol itu mewakili sesuatu yang tidak ada dan yang tidak ada itu ada, yakni nol. Siapa yang tidak bingung? Tiap kali bilangan nol muncul dalam pelajaran Matematika selalu ada ide yang aneh. Seperti ide jika sesuatu yang ada dikalikan dengan 0 maka menjadi tidak ada. Mungkinkah 5*0 menjadi tidak ada? (* adalah perkalian). Ide ini membuat orang frustrasi. Apakah nol ahli sulap?
Lebih parah lagi-tentu menambah bingung-mengapa 5+0=5 dan 5*0=5 juga? Memang demikian aturannya, karena nol dalam perkalian merupakan bilangan identitas yang sama dengan 1. Jadi 5*0=5*1. Tetapi, benar juga bahwa 5*0=0. Waw. Bagaimana dengan 5o=1, tetapi 50o=1 juga? Ya, sudahlah. Aturan lain tentang nol yang juga misterius adalah bahwa suatu bilangan jika dibagi nol tidak didefinisikan. Maksudnya, bilangan berapa pun yang tidak bisa dibagi dengan nol. Komputer yang canggih bagaimana pun akan mati mendadak jika tiba-tiba bertemu dengan pembagi angka nol. Komputer memang diperintahkan berhenti berpikir jika bertemu sang divisor nol.
Bilangan nol: tunawisma
Bilangan disusun berdasarkan hierarki menurut satu garis lurus. Pada titik awal adalah bilangan nol, kemudian bilangan 1, 2, dan seterusnya. Bilangan yang lebih besar di sebelah kanan dan bilangan yang lebih kecil di sebelah kiri. Semakin jauh ke kanan akan semakin besar bilangan itu. Berdasarkan derajat hierarki (dan birokrasi bilangan), seseorang jika berjalan dari titik 0 terus-menerus menuju angka yang lebih besar ke kanan akan sampai pada bilangan yang tidak terhingga. Tetapi, mungkin juga orang itu sampai pada titik 0 kembali. Bukankah dunia ini bulat? Mungkinkah? Bukankah Columbus mengatakan bahwa kalau ia berlayar terus-menerus ia akan sampai kembali ke Eropa?
Lain lagi. Jika seseorang berangkat dari nol, ia tidak mungkin sampai ke bilangan 4 tanpa melewati terlebih dahulu bilangan 1, 2, dan 3. Tetapi, yang lebih aneh adalah pertanyaan mungkinkan seseorang bisa berangkat dari titik nol? Jelas tidak bisa, karena bukankah titik nol sesuatu titik yang tidak ada? Aneh dan sulit dipercaya? Mari kita lihat lebih jauh.
Jika di antara dua bilangan atau antara dua buah titik terdapat sebuah ruas. Setiap bilangan mempunyai sebuah ruas. Jika ruas ini dipotong-potong kemudian titik lingkaran hitam dipindahkan ke tengah-tengah ruas, ternyata bilangan 0 tidak mempunyai ruas. Jadi, bilangan nol berada di awang-awang. Bilangan nol tidak mempunyai tempat tinggal alias tunawisma. Itulah sebabnya, mengapa bilangan nol harus menempel pada bilangan lain, misalnya, pada angka 1 membentuk bilangan 10, 100, 109, 10.403 dan sebagainya. Jadi, seseorang tidak pernah bisa berangkat dari angka nol menuju angka 4. Kita harus berangkat dari angka 1.
Mudah, tetapi salah
Guru meminta Ani menggambarkan sebuah garis geometrik dari persamaan 3x+7y = 25. Ani berpikir bahwa untuk mendapatkan garis itu diperlukan dua buah titik dari ujung ke ujung. Tetapi, setelah berhitung-hitung, ternyata cuma ada satu titik yang dilewati garis itu, yakni titik A(6, 1), untuk x=6 dan y=1. Sehingga Ani tidak bisa membuat garis itu. Sang guru mengingatkan supaya menggunakan bilangan nol. Ya, itulah jalan keluarnya. Pertama, berikan y=0 diperoleh x=(25-0)/3=8 (dibulatkan), merupakan titik pertama, B(8,0). Selanjutnya berikan x=0 diperoleh y=(25-3.0)/7=4 (dibulatkan), merupakan titik kedua C(0,4). Garis BC, adalah garis yang dicari. Namun, betapa kecewanya sang guru, karena garis itu tidak melalui titik A. Jadi, garis BC itu salah.
Ani membela diri bahwa kesalahan itu sangat kecil dan bisa diabaikan. Guru menyatakan bahwa bukan kecil besarnya kesalahan, tetapi manakah yang benar? Bukankah garis BC itu dapat dibuat melalui titik A? Kata guru, gunakan bilangan nol dengan cara yang benar. Bagaimana kita harus membantu Ani membuat garis yang benar itu? Mudah, kata konsultan Matematika. Mula-mula nilai 25 dalam 3x+7y harus diganti dengan hasil perkalian 3 dan 7 sehingga diperoleh 3x+7y=21.
Selanjutnya, dalam persamaan yang baru, berikan y=0 diperoleh x=21/3=7 (tanpa pembulatan) itulah titik pertama P(6,1). Kemudian berikan nilai x=0 diperoleh y=21/7 = 3 (tanpa pembulatan), itulah titik kedua Q(0, 3). Garis PQ adalah garis yang sejajar dengan garis yang dicari, yakni 3x+7y=25. Melalui titik A tarik garis sejajar dengan PQ diperoleh garis P1Q1. Nah, begitulah. Sang murid telah menemukan garis yang benar berkat bantuan bilangan nol.
Akan tetapi, sang guru masih sangat kecewa karena sebenarnya tidak ada satu garis pun yang benar. Bukankah dalam persamaan 3x1+7x2=25 hanya ada satu titik penyelesaian yakni titik A, yang berarti persamaan 3x1+7x2 itu hanya berbentuk sebuah titik? Bahkan pada persamaan 3x1+7x2=21 tidak ada sebuah titik pun yang berada dalam garis PQ. Oleh karena itu, garis PQ dalam sistem bilangan bulat, sebenarnya tidak ada. Aneh, bilangan nol telah menipu kita. Begitulah kenyataannya, sebuah persamaan tidak selalu berbentuk sebuah garis.
Bergerak, tetapi diam
Bilangan tidak hanya terdiri atas bilangan bulat, tetapi juga ada bilangan desimal antara lain dari 0,1; 0,01; 0,001; dan seterusnya sekuat-kuat kita bisa menyebutnya sampai sedemikian kecilnya. Karena sangat kecil tidak bisa lagi disebut atau tidak terhingga dan pada akhirnya dianggap nol saja. Tetapi, ide ini ternyata sempat membingungkan karena jika bilangan tidak terhingga kecilnya dianggap nol maka berarti nol adalah bilangan terkecil? Padahal, nol mewakili sesuatu yang tidak ada? Waw. Begitulah.
Berdasarkan konsep bilangan desimal dan kontinu, maka garis bilangan yang kita pakai ternyata tidak sesederhana itu karena antara dua bilangan selalu ada bilangan ke tiga. Jika seseorang melompat dari bilangan 1 ke bilangan 2, tetapi dengan syarat harus melompati terlebih dahulu ke bilangan desimal yang terdekat, bisakah? Berapakah bilangan desimal terdekat sebelum sampai ke bilangan 2? Bisa saja angka 1/2. Tetapi, anda tidak boleh melompati ke angka 1/2 karena masih ada bilangan yang lebih kecil, yakni 1/4. Seterusnya selalu ada bilangan yang lebih dekat... yakni 0,1 lalu ada 0,01, 0,001, ..., 0,000001. demikian seterusnya, sehingga pada akhirnya bilangan yang paling dekat dengan angka 1 adalah bilangan yang demikian kecilnya sehingga dianggap saja nol. Karena bilangan terdekat adalah nol alias tidak ada, maka Anda tidak pernah bisa melompat ke bilangan 2.
(sumber : forum.kompas.com/sains/16139-rahasia-angka-nol.html)
.jpg)


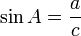

















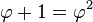
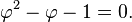
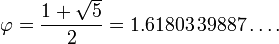




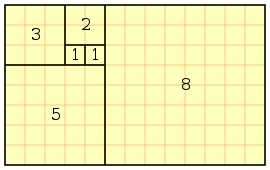
 Pisa mempelajari pemikiran tersebut dan mencocokkan dengan hasil penilitiannya terhadap perkembangbiakan kelinci. Populasi kelinci ternyata terus tumbuh dengan rasio yang itu-itu saja. Alhasil, muncullah kesimpulan berupa sebuah deret yang kemudian dinamakan Deret Fibonacci. (Mengenai penjelasan mengapa Pisa menggunakan kelinci dan mencocokkannya dengan hasil pemikiran Gopala Chandra, mungkin hanya Nobita dan Doraemon yang bisa mencari tahu. Dengan mesin waktunya, tentunya. Hehehehe! #random). Oh ya, ada pula yang berpendapat bahwa hasil pemikiran Gopala Chandra ini juga menjadi sejarah awal terciptanya permainan catur. #WhoKnows
Pisa mempelajari pemikiran tersebut dan mencocokkan dengan hasil penilitiannya terhadap perkembangbiakan kelinci. Populasi kelinci ternyata terus tumbuh dengan rasio yang itu-itu saja. Alhasil, muncullah kesimpulan berupa sebuah deret yang kemudian dinamakan Deret Fibonacci. (Mengenai penjelasan mengapa Pisa menggunakan kelinci dan mencocokkannya dengan hasil pemikiran Gopala Chandra, mungkin hanya Nobita dan Doraemon yang bisa mencari tahu. Dengan mesin waktunya, tentunya. Hehehehe! #random). Oh ya, ada pula yang berpendapat bahwa hasil pemikiran Gopala Chandra ini juga menjadi sejarah awal terciptanya permainan catur. #WhoKnows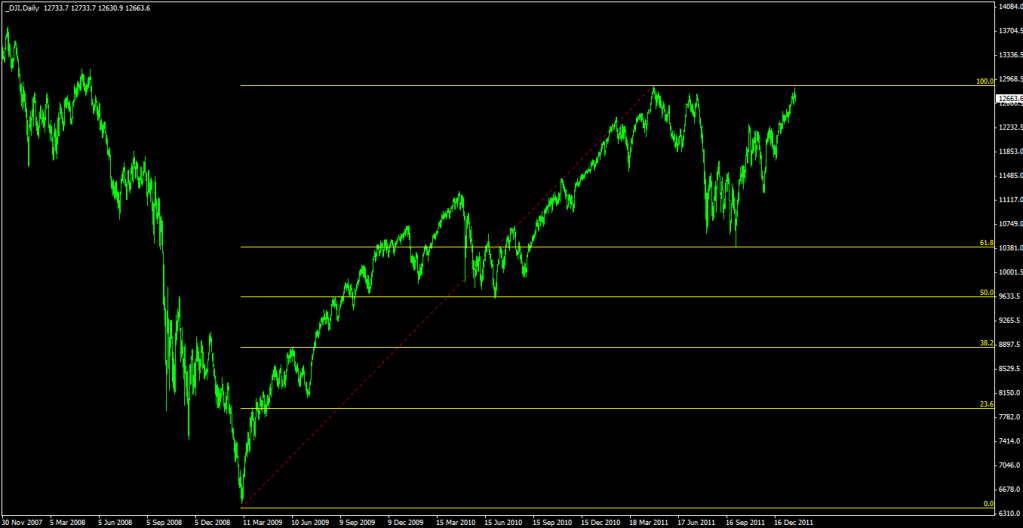 Gambar 2. Ini adalah tampilan mata uang $EURUSD sebelum dilakukan penarikan Fibonacci Retracement. Terlihat dengan jelas titik harga tertinggi dan terendah pada chart.
Gambar 2. Ini adalah tampilan mata uang $EURUSD sebelum dilakukan penarikan Fibonacci Retracement. Terlihat dengan jelas titik harga tertinggi dan terendah pada chart.